Hashing de Array (matrices)
En este capítulo, explicaremos cómo se realizan los hashings de Arrays (matrices) utilizando las funciones Pedersen y Poseidon en el contexto de Starknet. Estas operaciones son fundamentales para garantizar la integridad y seguridad de los cálculos realizados en el sistema.
El hashing de un array implica aplicar la función de hash correspondiente a cada elemento del array, de manera secuencial o iterativa. Esto permite resumir y representar de manera compacta la información contenida en el array, independientemente de su longitud o contenido específico.
El hashing de un array es útil en muchas aplicaciones, como la verificación de integridad de datos, la indexación eficiente de información y la identificación única de elementos.
Pedersen
La función hash Pedersen, denotada como h, se utiliza para calcular el hash de un array de elementos de campo. Consideremos un arreglo a₁, a₂, ..., aₙ que contiene n elementos. La definición de h(a₁ a₂, ..., aₙ) es la siguiente:
- Comenzamos con un valor inicial de 0.
- Aplicamos la función de hash h al primer elemento a₁ junto con el valor inicial. El resultado se convierte en el nuevo valor inicial.
- Continuamos aplicando la función de hash h al siguiente elemento a₂ junto con el valor anteriormente obtenido. Nuevamente, el resultado se convierte en el nuevo valor inicial.
- Repetimos este proceso hasta llegar al último elemento aₙ, aplicando la función de hash en cada paso.
- Finalmente, aplicamos la función de hash h al último elemento an junto con el valor obtenido en el paso anterior.
De esta manera, obtenemos el resultado final que representa el hash del array completo.

Esta construcción en capas nos permite combinar de manera secuencial los elementos del array a medida que calculamos el hash. Cada iteración agrega un nivel adicional de seguridad y complejidad al resultado final.
Poseidon
La función de hash Poseidon utiliza la permutación Hades, representada por hades: 𝔽³ₚ→𝔽ₚ, con los parámetros de Starknet. Dado un array a₁, a₂, ..., aₙ que contiene n field elements, definimos poseidon(a₁, a₂, ..., aₙ) como la primera coordenada de H(a₁, a₂, ..., aₙ; 0, 0, 0),
H(a₁, a₂, ..., aₙ; s₁, s₂, s₃)se define de la siguiente manera:
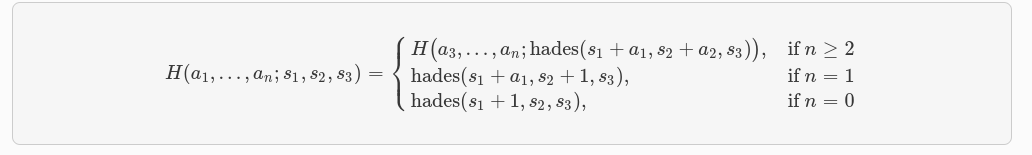
- Si n ≥ 2: entonces
H(a₁,a₂,...,aₙ;s₁,s₂,s₃) = H(a₃, a₄, ..., aₙ;hades(s₁ + a₁, s₂ + a₂, s₃)). - Si n = 1: entonces
H(a₁; s₁, s₂, s₃) = hades(s₁ + a₁, s₂ + 1, s₃). - Si n = 0: entonces
H(); s₁, s₂, s₃) = hades(s₁ + 1, s₂, s₃).
En resumen, la función poseidon(a₁,a₂,...,aₙ) toma el array de field elements y aplica la permutación Hades en capas. Cada iteración de la permutación combina los elementos del array en función de los valores de s₁, s₂ y s₃, generando así una salida única. La primera coordenada de la salida final se considera el resultado de la función de hash Poseidon.
Esta construcción en capas y la utilización de la permutación Hades permiten obtener un hash seguro y resistente a ciertos ataques criptográficos.